Цифровые аудио сигналы 

Компьютер – это цифровое устройство, то есть электронное устройство, в котором рабочим сигналом является дискретный сигнал. Сегодняшние компьютеры оперируют дискретными сигналами, несущими двоичные значения, условно обозначаемые как «да» и «нет» (на электрическом уровне: 0 вольт и V вольт, для некоторого ненулевого значения V). С помощью одного двоичного сигнала за один шаг можно передать информацию об одном из всего двух положений: 0 («да») или 1 («нет»). С помощью N двоичных сигналов за один шаг можно передать информацию об одном из 2 N положений (2 N – это число комбинаций нулей и единиц для N сигналов). Взаимодействие всех составляющих компьютер блоков происходит путем обмена и обработки одним или одновременно несколькими двоичными сигналами. Все – коды управления, а также сама обрабатываемая информация – все представляется в компьютере в виде чисел. По этой причине и аудио сигналы в цифровой аппаратуре представляют в виде чисел.

Итак, каким же образом можно описать аналоговый аудио сигнал в цифровой форме? Реальный аудио сигнал – это сложное по форме колебание, некая сложная зависимость амплитуды звуковой волны от времени. Преобразование аналогового звукового сигнала в цифровой вид называется аналогово-цифровым преобразованием или оцифровкой. Процесс такого преобразования заключается в:

· осуществлении замеров величины амплитуды аналогового сигнала с некоторым временным шагом - дискретизация;

· последующей записи полученных значений амплитуды в численном виде – квантование.

 

Дискретизация

 

Процесс дискретизации по времени - это процесс получения мгновенных значений преобразуемого аналогового сигнала с определенным временным шагом, называемым шагом дискретизации (см. рис. 7).

 

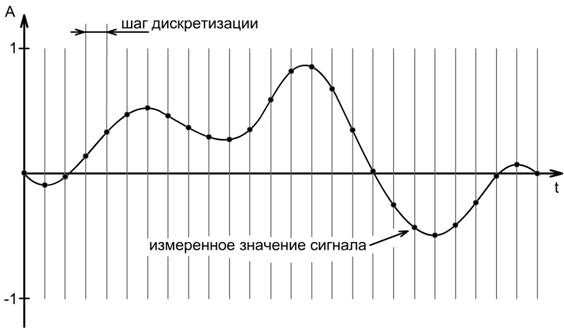
Количество осуществляемых в одну секунду замеров величины сигнала называют частотой дискретизации или частотой выборки, или частотой сэмплирования (от англ. « sampling» – «выборка»). Очевидно, что чем меньше шаг дискретизации, тем выше частота дискретизации (то есть, тем чаще регистрируются значения амплитуды), и, значит, тем более точное представление о сигнале мы получаем. Это рассуждение подтверждается доказанной теоремой, теоремой Котельникова (в зарубежной литературе встречается как теорема Шеннона, Shannon). Согласно этой теореме, аналоговый сигнал с ограниченным спектром может быть точно описан дискретной последовательностью значений его амплитуды, если эти значения следуют с частотой, как минимум вдвое превышающей наивысшую частоту спектра. Иначе говоря, аналоговый сигнал, в котором частота наивысшей составляющей спектра равна F m, может быть точно описан последовательностью дискретных значений амплитуды, если для частоты дискретизации F d выполняется: . На практике это означает следующее: для того, чтобы оцифрованный сигнал содержал информацию о всем диапазоне слышимых человеком частот исходного аналогового сигнала (0 – 20 кГц) необходимо, чтобы выбранное значение частоты дискретизации при оцифровке сигнала составляло не менее 40 кГц.

Казалось бы, для завершения процесса оцифровки теперь осталось лишь записать измеренные мгновенные значения амплитуды сигнала в численной форме. Полученная последовательность чисел (по одному результату замера амплитуды сигнала на каждый шаг) и образует цифровую форму исходного аналогового сигнала – так называемый импульсный сигнал . Здесь, однако, обнаруживается основная трудность оцифровки, заключающаяся в невозможности записать измеренные значения сигнала с идеальной точностью.

 

Линейное (однородное) квантование

 

Допустим, что для записи одного значения амплитуды сигнала в памяти компьютера мы отводим N бит. Соответственно, с помощью одного N -битного слова (слово – последовательность N бит) можно описать 2 N разных положений. Допустим теперь, что амплитуда оцифровываемого сигнала колеблется в пределах от -1 до 1 некоторых условных единиц. Заметим, что измеренным значениям амплитуды ничто не мешает быть дробными (например, -0.126 или 0.997). Представим этот диапазон изменения амплитуды - динамический диапазон сигнала - в виде 2 N -1 равных промежутков, разделив его на 2 N уровней - квантов (произведя таким образом однородное, линейное разбиение амплитудной шкалы). Теперь, для записи каждого отдельного значения амплитуды, его необходимо округлить до ближайшего уровня квантования. Этот процесс называется квантованием по амплитуде. Говоря более формальным языком, квантование по амплитуде – это процесс замены реальных (измеренных) значений амплитуды сигнала значениями, приближенными с некоторой точностью. Каждый из 2 N возможных уровней называется уровнем квантования,а расстояние между двумя ближайшими уровнями квантования называется шагом квантования. В случае линейного разбиения амплитудной шкалы на уровни, квантование называют линейным (однородным) . На рис. 8 представлен пример такого квантования.

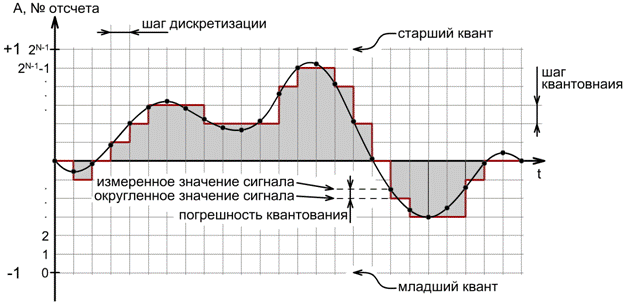
Как видно, результатом такой оцифровки стал ступенчатый сигнал, составленный из прямоугольников, каждый из которых имеет ширину равную величине шага дискретизации, и высоту равную измеренному значению амплитуды сигнала.

Очевидно, что точность округления зависит от выбранного количества (2 N) уровней квантования, которое, в свою очередь, зависит от количества бит ( N), отведенных для записи значения амплитуды. Чем больше уровней квантования и чем ближе они друг к другу (а, для некоторого фиксированного диапазона изменения амплитуды расстояние между уровнями квантования обратно пропорционально их количеству), тем на меньшую величину приходится округлять измеренные значения амплитуды, и, таким образом, тем меньше получаемая погрешность квантования. Число N называют разрядностью квантования (подразумевая количество разрядов, то есть бит, в каждом слове), а полученные в результате округления значений амплитуды числа – отсчетами или сэмплами (от англ. “ sample” – “замер”).Считается, что погрешность квантования, являющаяся результатом квантования с разрядностью 16 бит, остаются для слушателя почти незаметными.

Описанный способ оцифровки сигнала - дискретизация сигнала во времени в совокупности с методом однородного квантования - называется импульсно-кодовой модуляцией, ИКМ (англ. Pulse Code Modulation – PCM). Стандартный аудио компакт-диск ( CD- DA), применяющийся с начала 80-х годов 20-го столетия, хранит информацию в формате PCM, с частотой дискретизации 44.1 кГц и разрядностью квантования 16 бит.

 

 

Сложности, связанные с оцифровкой

 

Не смотря на кажущуюся простоту и интуитивность процесса оцифровки, эта процедура сопряжена со многими трудностями и проблемами.

Во-первых, частота дискретизации, устанавливаемая теоремой Котельникова, является минимально необходимой, но не достаточной. Дискретизация вносит дополнительные помехи в спектр исходного сигнала, добавляя в него его же зеркальную копию. Поэтому значение частоты дискретизации должно выбираться несколько большим, чем частота, устанавливаемая теоремой Котельникова, чтобы сделать возможной успешную фильтрацию лишних спектральных составляющих.

Во-вторых, квантование значений сигнала привносит в спектр сигнала дополнительную помеху, называемую шумом квантования или шумом дробления . Шумом (ошибкой) квантования называют сигнал, составляющий разницу между восстановленным цифровым и исходным аудио сигналами. Эта разница образуется в результате округления измеренных значений сигнала. При этом выполняется следующая закономерность: чем выше разрядность квантования, тем ниже уровень шума квантования (поскольку тем на меньшее значение требуется округлять каждое измеренное значение сигнала). Природа шума квантования такова, что ширина спектральной области, в которой он простирается, пропорциональна значению частоты дискретизации. При этом при фиксированной разрядности квантования, общая энергия шума квантования остается постоянной. А это значит, что чем выше частота дискретизации, тем в более широкой спектральной области простирается шум квантования и, соответственно, тем ниже его мощность в некоторой фиксированной интересующей нас полосе спектра, например, в полосе слышимых частот. Этот факт имеет большое практическое значение.

Надо сказать, что уровень шума квантования также зависит и от формы самого сигнала. В идеальном случае, ошибка при округлении значений сигнала является случайной и, значит, спектр шума квантования оказывается равномерным. В реальности, однако, этого не происходит. Форма реальных звуковых сигналов является в определенной степени не случайной, а, значит, и ошибка квантования тоже является не случайной. В этом случае спектр шума квантования оказывается не равномерным и концентрируется в какой-то определенной области, что отрицательно сказывается на звучании цифрового сигнала. Существует несколько способов борьбы с этим явлением. Так, нежелательную концентрацию шума квантования в некоторой частотной области можно нейтрализовать путем подмешивания к исходному аналоговому сигналу некоторого слабого по мощности псевдослучайного шума. Этот шум минимизирует степень зависимости ошибок округления от формы преобразуемого сигнала, что хорошо рассеивает спектр шума квантования и делает его равномерным. Таким образом, описанный прием (называемый дизерингом, от англ. « dithering» – «дрожание») как бы подменяет нежелательный шум квантования искусственно подмешанным псевдослучайным шумом. При этом подмешанный псевдослучайный шум оказывается менее заметным на слух, чем тот шум квантования, какой получился бы без применения дизеринга. Еще один прием борьбы с уровнем шума квантования называется формовкой шума (от англ. “ noise shaping”). Идея приема заключается в преднамеренном изменении формы исходного аналогового сигнала специальным образом, чтобы последующее квантование привело к появлению шума квантования, основная энергия которого расположилась бы в наименее заметных на слух частотных областях. Формирование шума с таким спектром достигают путем использования фильтра, моделирующего кривую равной громкости (об этой кривой мы говорили выше).

Импульсный сигнал, получаемый в результате аналогово-цифрового преобразования, из-за несовершенности преобразующих устройств имеет некоторые изъяны. Эти изъяны выражаются в случайных отклонениях длительностей прямоугольных импульсов от номинальной величины шага дискретизации, а также в неабсолютной крутизне фронтов импульсов. Говоря иначе, осуществление выборки сигнала при оцифровке происходит не через абсолютно равные промежутки времени, а с некоторыми случайными отклонениями от номинала, при этом результирующий импульсный сигнал вдобавок имеет неидеальную прямоугольную форму. Если, скажем, дискретизация проводится с частотой 44.1 кГц, то отсчеты берутся не точно каждые секунды, а то чуть раньше, то чуть позднее. А так как входной сигнал постоянно меняется, то такая погрешность приводит к регистрации не совсем верного уровня сигнала. Описанный неприятный эффект называется джиттером (от англ. « jitter» – «дрожание») и по сути является исключительно результатом неабсолютной стабильности аппаратуры (АЦП). На слух джиттер воспринимается как некоторое дрожание сигнала на высоких частотах, при этом на низких частотах джиттер выражается в некотором «размазывании» спектра сигнала. Для борьбы с джиттером применяют высокостабильные тактовые генераторы. Следует заметить, что причиной появления джиттера может быть не только аналогово-цифровое преобразование, но и передача импульсного сигнала по цифровому каналу от одного устройства к другому. В этом случае появление джиттера является результатом неидеальной коммутации/синхронизации устройств и может быть устранено только путем использования аппаратуры, регенерирующей цифровой сигнал.

Рассмотрим, наконец, еще один неприятный эффект оцифровки, называемый гранулярным шумом. Гранулярным шумом(от англ. « granular noise») называют эффект нестабильности округления в процессе квантования. Если величина сигнала незначительно меняется около некоторой величины, являющейся границей между двумя соседними уровнями квантования, даже самые маленькие колебания величины сигнала вокруг этой границы могут вызывать заметные изменения результатов округления при квантовании значений амплитуды. Это связано с тем, что квантователь в этом случае округляет измеренное значение сигнала то до величины одного, то до величины второго из соседствующих уровней квантования.